Rosenbrock function and Curve fiting

The Rosenbrock function

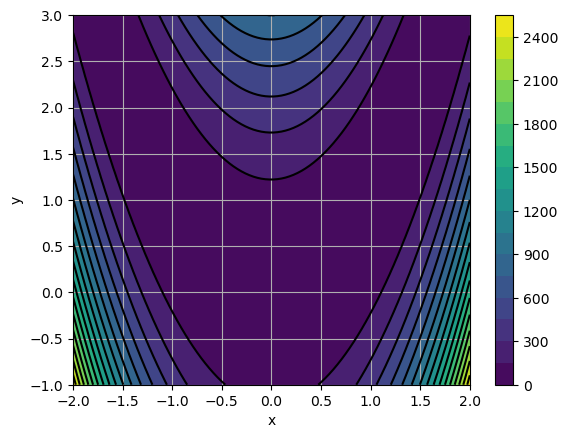
The Rosenbrock function is a classical benchmark for optimization algorithms. It is defined by the following equation:

\[ f(x, y) = (1-x)^2 + 100 (y-x^2)^2 \]

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt


def Rosen(X):
    """
    Rosenbrock function
    """
    x, y = X
    return (1 - x) ** 2 + 100.0 * (y - x**2) ** 2


x = np.linspace(-2.0, 2.0, 100)
y = np.linspace(-1.0, 3.0, 100)
X, Y = np.meshgrid(x, y)
Z = Rosen((X, Y))

fig = plt.figure(0)
plt.clf()
plt.contourf(X, Y, Z, 20)
plt.colorbar()
plt.contour(X, Y, Z, 20, colors="black")
plt.grid()
plt.xlabel("x")
plt.ylabel("y")
plt.show()

Questions

1. Find the minimum of the function using brute force. Comment the accuracy and number of function evaluations.

2. Same question with the simplex (Nelder-Mead) algorithm.

Curve fitting

Questions

1. Chose a mathematical function \(y = f(x, a, b)\) and code it.

2. Chose target values of \(a\) and \(b\) that you will try to find back using optimization.

3. Evaluate it on a grid of \(x\) values.

4. Add some noise to the result.

5. Find back \(a\) and \(b\) using curve_fit